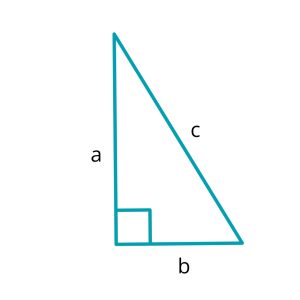What is Pythagoras Theorem?

Pythagoras’ Theorem states: In a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

This mathematical gem can be expressed as:

a² + b² = c²

Here, c represents the length of the hypotenuse, while a and b denote the lengths of the other two sides. If you are not sure which is the hypotenuse, check out our other blog post about an introduction to Trigonometry

It is important to note that this is only for right angle triangles. It can also be written as:

c² = a^² + b²

which is the same as:

c² – a² = b²

c² – b² = a²

Visualising and Understanding the Theorem:

Pythagoras’ theorem is talking about the square of each side (the length times it’s self).

Playing with square cut outs can help you better understand this theorem and test it for yourself.

Here you can see squares that have the same side length as the sides of a right angle triangle. We have coloured the square of the hypotenuse in red.

When we compare their size, we can see what Pythagoras was saying. The square of the length of the hypotenuse (in red) is equal to the sum of the squares of the lengths of the other two sides.

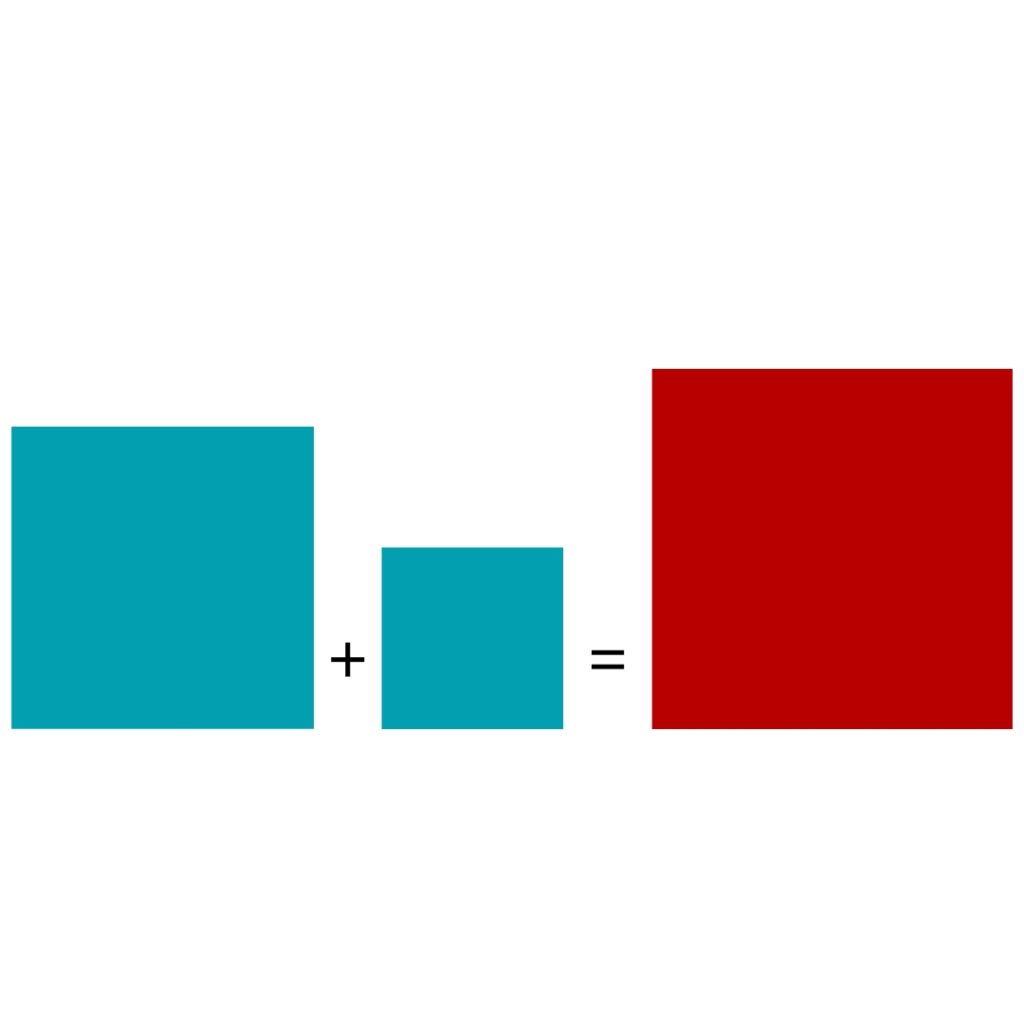
You may want to experiment with this for yourself to test it in detail, but hopefully with the illustration above you can see that it is true, the red square is equal in sizes to the two blue squares combined.

Understanding this will help you avoid a common pitiful of adding the length of the two sides which dose NOT equal the length of the hypotenuse. We can see that in the illustration below:

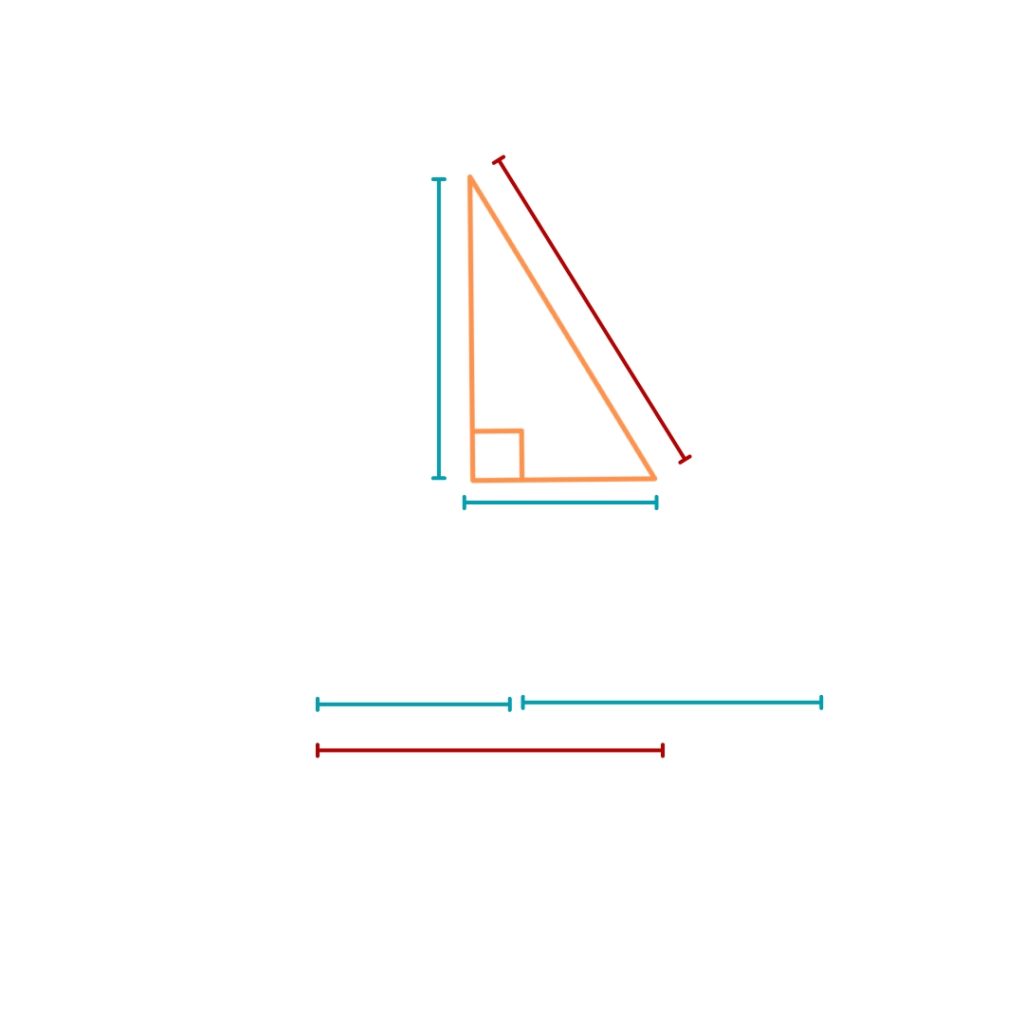
The Origin Story:

Pythagoras’ Theorem owes its name to the ancient Greek mathematician and philosopher Pythagoras, who lived around 570–495 BCE. Born on the island of Samos, Pythagoras founded a school in Croton, Italy, where he and his followers explored the profound connections between numbers and shapes.

Practical Applications:

Construction and Architecture:
- Builders and architects employ Pythagoras’ Theorem to ensure precise measurements in construction, ensuring the stability and accuracy of structures.
Navigation:
- Nautical navigation relies on the theorem for determining distances and coordinates, enabling sailors to chart accurate courses.
Physics:
- The theorem is integral to physics, aiding in calculations related to force vectors and motion.
Technology:
- Engineers use the theorem in designing electronic circuits, antennas, and other technological applications.