Pythagoras' Theorem: Practice Questions with Answers & Explanations [Year 10 Maths]

In Year 10 standard maths students are expected to master basic trigonometry and understand Pythagoras’ theorem. Today we’ll dive into the practical side of Pythagorean calculations, exploring example questions and how to work out their answers. We will take things step by step, with writen explanations as we go.

In previous blog posts we have covered:

If you need to revise any of those topics it is best to do so before exploring these example questions.

Let’s get started:

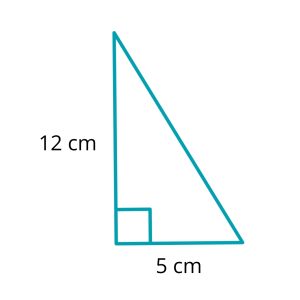
Example 1: Finding the Hypotenuse Length

Question: In a right-angled triangle, one side measures 5cm, and the other side measures 12cm. What is the length of the hypotenuse?

Solution:

c² = a² + b²	This is Pythagoras’ Theorem. We are trying to find c the hypotenuse
c² = 5² + 12²	Put in the two sides whose length we do know
c² = 25 + 144	Square the two sides first (5 x 5 = 25, 12 x 12 = 144)
c² = 169	Then add the results together
c = √169	To find c rather than c² we need to take the square root (169 = 13 x 13)
c = 13	And now we know the answer. The length of the hypotenuse is 13cm.

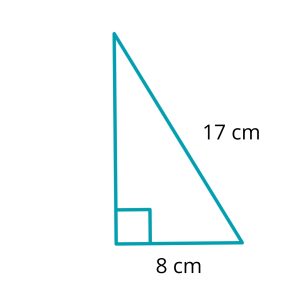
Example 2: Calculating a Missing Side

Question: In a right-angled triangle with a hypotenuse of length 17 cm and one side measuring 8 cm, what is the length of the other side?

Solution:

c² = a² + b²	This is Pythagoras’ Theorem. We are trying to find b one of the side lengths
17² = 8² + b²	Put in the two sides whose length we do know
289 = 64 + b²	Square the two sides first (17 x 17 = 289, 8 x 8 = 64)
289 – 64 = b²	Subtract 64 from both sides of the equation
225 = b²	Almost done!
√225 = b	To find b rather than b² we need to take the square root (225 = 15 x 15)
15 = b	And now we know the answer. The length of the other side is 15cm.

Example 3: Real word example without a diagram

Question: If a ladder of length 5m is resting on a wall of length 4m, then find the distance between the foot of the ladder and the bottom of the wall.

Solution:

We can assume the wall meets the ground at a right angle so Pythagoras’ theorem will apply to the triangle created by the wall, the ground, and the ladder.

The wall height will be one side, the ladder will be the hypotenuse, and we are looking for the distance between the wall and the foot of the ladder (the other side of the triangle).

You may find it helpful to create a sketch to better understand the problem. Or you can simply jump right in to the equation.

c² = a² + b²	This is Pythagoras’ Theorem. We are trying to find b one of the side lengths.
5² = 4² + b²	Put in the two sides whose length we do know. The ladder length is the hypotenuse (5m), and the wall height is one side (4m).
25= 16 + b²	Square the two sides first (5 x 5 = 25, 4 x 4 = 16)
25 – 16 = b²	Subtract 25 from 16 in order to move it to the other side of the equation (c² = a² + b² is the same as c² – a² = b²)
9 = b²	25 – 16 = 9
√9 = b	To find b rather than b² we need to take the square root (9 = 3 x 3)
3 = b	And now we know the answer. The distance between the foot of the ladder and the bottom of the wall is 3m.

How did you go?

Often when we are struggling with a new concept, seeing it broken down step by step can unlock an understanding we hadn’t been able to grasp before.

If there are things you don’t understand in these examples, seeing the step by step will also allow you to ask questions from you teacher, peers or tutor and point to exactly where you are getting lost. If you still need help we recommend a tutor to talk you through your understanding and help you on your way.