6 Steps to Apply Pythagoras' Theorem

In our last blog post we looked at what is Pythagoras’ theorem and made sure we were clear about our understanding of it and how it works. Today we will take a closer look at how to apply this theorem to find the length of the side of a right angle triangle. We can do this in 6 predictable steps.

How to Apply Pythagoras’ Theorem

Most of the time you will be given the length of two sides of a right angle triangle, and asked to find the length of remaining side.

Occasionally you will be given a real word scenario where you need to figure out how to apply the information provided. In that case it can be helpful to draw out the scenario in order to better visualise the triangle in question.

For today’s example we use a real world scenario as it is more complex so will better equip you for difficult questions you may encounter.

Either way, there are 6 steps that are relatively straight forward to follow. Let’s jump in:

Step By Step Instructions

Step 1

Write out Pythagoras’ theorem. You can do this simply as a² + b² = c² or you may choose to arrange the formulae to focus on what you are trying to find.

For example, you are trying to find the height of a building and you know you are 10 m away from the base of it on flat ground, and you also happen to know that a string from near your feet to the top of the building would measure 15 m. You can choose to leave the formulae as is or you may want to rearrange it to focus on a (the height of the building) like so

a² = c² – b²

You may like to draw yourself a diagram to better understand the situation:

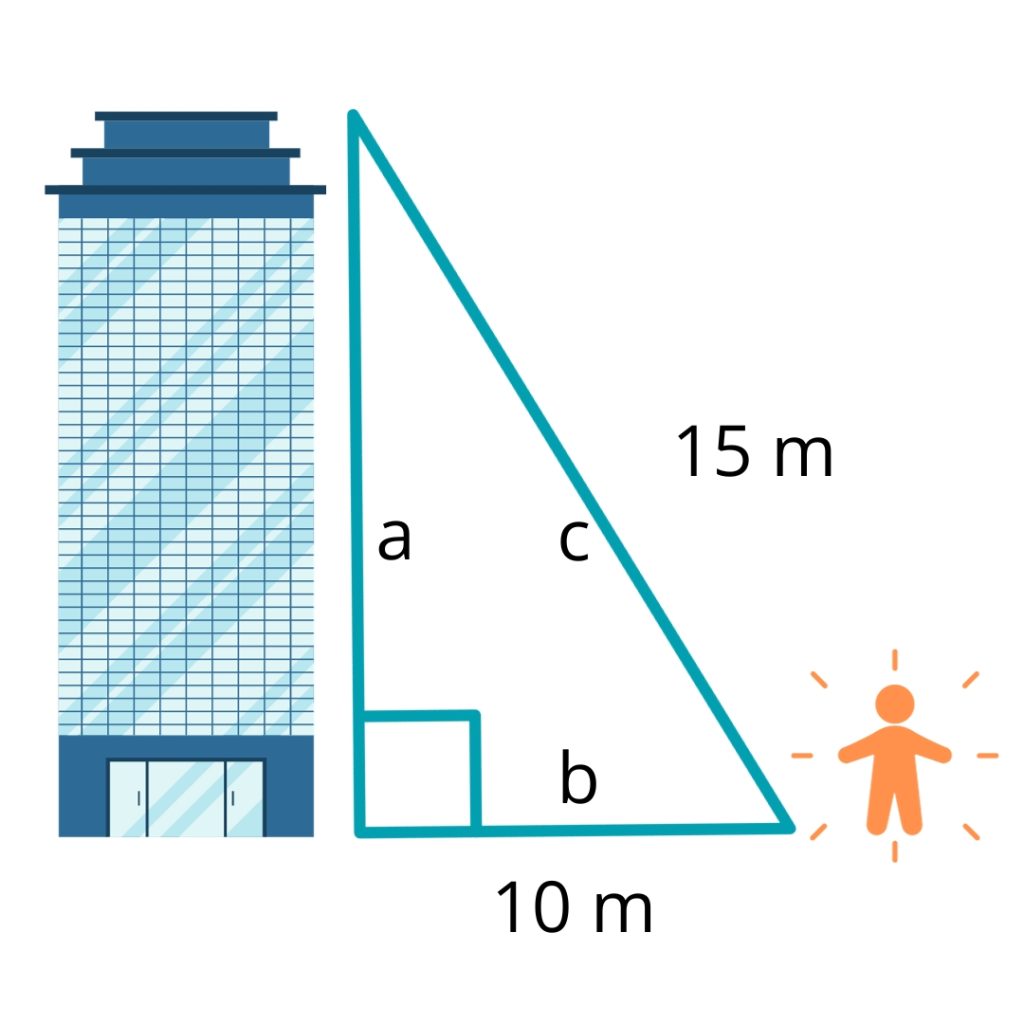
Step 2

Put in the information that you do know.

In this example we know the distance from us to the base of the building (b) and the distance from our feet to the top of the building (the hypotenuse, c) so we can enter that information into our formulae.

It may look like this:

15² = a² + 10²

Or like this:

a² = 15² – 10²

depending on what you chose to do in step one. Both are equal and it is simply matter of preference.

Step 3

The next step is to square the side lengths. It is important to do this before any addition and subtraction.

10 x 10 = 100 and 15 x 15 = 225 so our equation will look like:

225 = a^² + 100

or could be written as

a² = 225 – 100

Step 4

Then we do the addition or subtraction as required. With our first option we need to subtract 100 from both sides, leaving us with

125 = a²

which is the same as our second option

a² = 125.

Step 5

Step 5 is to take the square root of both sides. Since we are NOT looking a² but just a itself; the height of the building not the square of the height of the building.

With assistance of a calculator we can see that √125 = 11.180 to 3 decimal places.

a = 11.180

Step 6

Now we know the answer. The building is just over 11 m tall.

We may need to put back any unit measurements such as mm, cm, m, km in order to receive full marks and to make sure our answer makes sense in the context of the question. We may also need to check how accurate we were asked to be (perhaps the question said to two decimal places, or asked us to give a simplified square root such as 5√5).

Rereading the question and making sure we have satisfied the requirements is always a clever idea.

See More Examples

In our next blog post we will go over some practice questions with answers & explanations. Reading these and then practicing on your own is a great way to make sure you have a solid understanding of Pythagoras’ theorem and how to apply it.